Características del Continuo

Imagino que casi cualquiera que haya pasado por este blog estará al tanto de que hay problemas en Teoría de Conjuntos que son independientes de los axiomas actualmente aceptados ($\mathit{ZFC}$). El más famoso, por lejos, es la

Hipótesis del Continuo ($\mathit{CH}$): Todo subconjunto no numerable de $\mathbb{R}$ es biyectivo con $\mathbb{R}$.

El cardinal de $\mathbb{N}$ se escribe $\aleph_0$ y se puede probar que hay un mínimo cardinal no numerable, $\aleph_1$. El cardinal de $\mathbb{R}$ es igual al cardinal de todas las funciones de $\mathbb{N}$ en $2=\{0,1\}$, y por ello lo llamamos $2^{\aleph_0}$, o bien $\mathfrak{c}$ (por “el continuo”). Como $\mathbb{R}$ no es numerable, tiene subconjuntos de tamaño $\aleph_1$. Por tal motivo, la forma más cortita de enunciar $\mathit{CH}$ es escribir $2^{\aleph_0} =\aleph_1$: no hay cardinales entre el de $\mathbb{N}$ y el de $\mathbb{R}$.

$\mathit{CH}$ no se puede probar ni refutar con los axiomas actuales (a menos que sean inconsistentes, i.e. lleven a contradicciones). En general, los axiomas de $\mathit{ZFC}$ no determinan en qué posición de la “recta cardinal” está el conjunto de los números reales: no deciden si es igual a $\aleph_1$, o $\aleph_5$, o si acaso es menor que $\aleph_{31415}$. El “monstruo feo de la incompletitud” (como decía Erdös) muestra su peor cara con este problema.

En esta situación, como en otras relativamente similares, una estrategia razonable es averiguar qué relación tiene $\mathfrak{c}$ con otros cardinales, llamados características cardinales del continuo, que resultan de estudiar objetos relacionados con $\mathbb{R}$. Entre ellos se encuentran $\mathcal{P}(\mathbb{N})$, ${}^\mathbb{N}2$ (funciones de $\mathbb{N}$ en el $2$), ${}^\mathbb{N}\mathbb{N}$, y otros más, que son canónicamente biyectivos entre sí. Las características cardinales son siempre no numerables y menores o iguales a $\mathfrak{c}$. En diversos universos de $\mathit{ZFC}$, las características pueden tener valores distintos dos a dos y a su vez distintos de $\aleph_1$, $\mathfrak{c}$. Por tal motivo, estas características se las llama “invariantes cardinales”, puesto que determinan parte de la estructura cardinal de dichos universos.

En un universo donde vale $\CH$, todas las características colapsan a $\mathfrak{c}$. En un próximo post nos dedicaremos al Axioma de Martin ($\MA$), que tiene esta misma consecuencia pero por razones completamente diferentes. Lo más interesante de $\MA$ es que los conceptos involucrados en su definición y uso son los mismos que se utilizan en la técnica de forzamiento o forcing, una de las principales para demostrar resultados de independencia de $\ZFC$. Presentar forcing usando $\MA$ ya es estándar (por ejemplo, en Kunen ^[1] y su clásico ^[2]).

Este post está basado en parte en las notas de un curso dictado por Justin Palumbo ^[3].

1. Dominación de funciones

La primera característica del continuo que introduciremos resulta de estudiar la relación de dominación eventual entre funciones de $\mathbb{N}$ en $\mathbb{N}$.

Es decir, si $g$ domina a $f$ entonces es “casi siempre mayor”. En general, también se pueden definir $\leq^*$, $=^*$, y resulta que $f< ^* g \leftrightarrow f\leq^*g \wedge f (\neq)^* g$.

Es fácil ver que toda familia finita de funciones $\{f_i : i< k\}$ está acotada, es decir, se puede dominar: basta tomar $g(n)\mathrel{\mathop:}= \max\{f_i(n) : i< k\} +1$. Por otro lado, el orden $< ^*$ sobre ${}^\mathbb{N}\mathbb{N}$ es mucho más interesante que el orden $<$ punto a punto. De hecho, una diferencia es la siguiente:

Esto nos lleva a preguntarnos, ¿cuántas funciones pueden dominarse a la vez?

Dado que ${}^\mathbb{N}\mathbb{N}$ no se puede dominar, es inmediato que $\aleph_0< \mathfrak{b}\leq 2^{\aleph_0}$ y $\mathit{CH}$ implica $\mathfrak{b}= 2^{\aleph_0}$.

2. Familias casi disjuntas

La segunda característica que introduciremos surge de considerar “casi particiones” de $\mathbb{N}$.

El nombre “loca” proviene de la traducción de la siglas mad del inglés “maximal almost disjoint”. Como consecuencia de la definición, si $\mathcal{F}$ es loca y $X\subseteq\mathbb{N}$ es infinito, hay $A\in\mathcal{F}$ tal que $A\cap X$ es infinito.

Aunque parezca, este lema no requiere ninguna forma de $\AC$.

Luego, podemos definir

$\displaystyle \mathfrak{a} \mathrel{\mathop:}= \min\{|\mathcal{F}| : \mathcal{F} \text{ es loca}\},$

y concluimos que $\ale0< \mathfrak{a}\leq2^{\ale0}$.

3. Una desigualdad

Las dos características que introdujimos no son independientes entre sí.

Prueba. Sea $\ka$ un conjunto de índices de cardinal menor a $\mathfrak{b}$. Veremos que ninguna familia casi disjunta indizada por $\ka$ puede ser maximal. Asumimos que $\mathbb{N}\subseteq \ka$.

(De hecho, usualmente en Teoría de Conjuntos, cada cardinal $\la$ es naturalmente un conjunto de tamaño $\la$, y está bien ordenado de manera que tiene un segmento inicial isomorfo a $\mathbb{N}$. Los dos elementos siguientes a todos los naturales se denotan con $\omega$ y $\omega+1$, y los usaremos más abajo como elementos de $\ka\sm\N$).

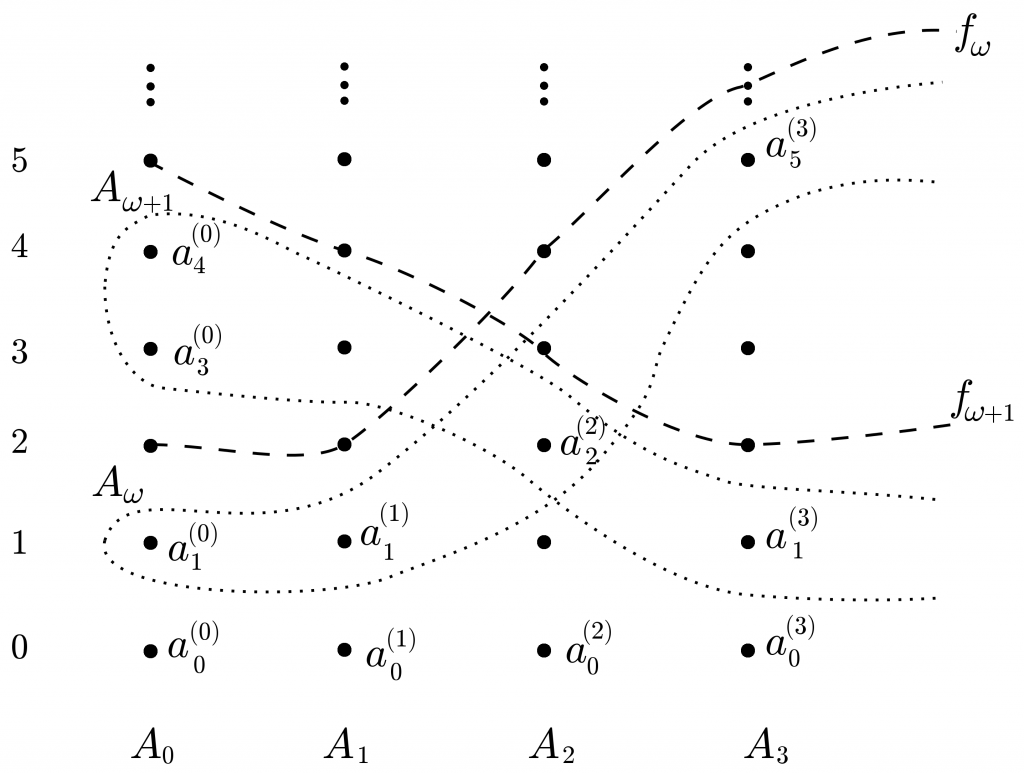
Sea $\mathcal{F} = \{A_\alpha : \alpha\in\ka\}$. Por la observación ($\nabla$), podemos suponer que $\{A_\alpha : \alpha\in\mathbb{N}\}$ son disjuntos dos a dos. Enumeramos cada $A_n$ ($n\in\mathbb{N}$) de manera creciente: $A_n=\bigl\{a_m^{(n)} : m\in\mathbb{N}\bigr\}$, con $a_m^{(n)}< a_{m+1}^{(n)}$ para todo $m$ y definamos, para $\alpha\in\ka\sm\mathbb{N}$,

$\displaystyle f_\alpha(n)\mathrel{\mathop:}= \min\bigl\{m: A_n\cap A_\alpha < a_m^{(n)}\bigr\}.$

En la Figura se ve cómo se definen estas funciones. Los conjuntos $A_n$ con $n\in\mathbb{N}$ están dispuestos verticalmente, y son cortados “transversalmente” por los $A_\alpha$ con $\alpha\in\ka\sm\mathbb{N}$ (en líneas punteadas). Esta terminología tiene sentido porque cada intersección $A_n\cap A_\alpha$ es finita. Luego, el valor de $f_\alpha(n)$ es el índice del menor elemento de $A_n$ que acota estrictamente a dicha intersección. En el ejemplo, tenemos los valores indicados en la Tabla.

$n$		$0$	$1$	$2$	$3$	…
$f_\omega$		$2$	$2$	$4$	$6$	…
$f_{\omega+1}$		$5$	$4$	$3$	$2$	…

Prosiguiendo con el argumento, tenemos una familia de menos de $\mathfrak{b}$ funciones, así que hay una $f:\mathbb{N}\rightarrow\mathbb{N}$ que las domina a todas. Definamos entonces $B\mathrel{\mathop:}=\bigl\{a_{f(n)}^{(n)}: n\in\mathbb{N}\bigr\}$; por construcción, $A_n\cap B =\bigl\{a_{f(n)}^{(n)}\bigr\}$. Veremos que $B$ es casi disjunto de todos los $A_\alpha$.

Sea $\alpha\in\ka\sm\mathbb{N}$. Como $f_\alpha< ^* f$, existe $n_0$ tal que $\forall n\geq n_0$, $f_\alpha(n)< f(n)$. Esto implica que

$\displaystyle a_{f_\alpha(n)}^{(n)}< a_{f(n)}^{(n)}\in A_n.$

Como $a_{f_\alpha(n)}^{(n)}$ es cota superior de $A_n\cap A_\alpha$, concluimos que $a_{f(n)}^{(n)}\notin A_\alpha$. Luego

$\displaystyle A_\alpha\cap B\subseteq\bigl\{a_{f(m)}^{(m)} : m < n_0\bigr\},$

obviamente un conjunto finito. $\Box$

Es consistente que se dé $\mathfrak{b}=\mathfrak{a}$, pero también lo es (por un teorema de S. Shelah) que no coincidan.

References

1. K. Kunen (2011): Set Theory. Second, College Publications, 2011, ISBN: 9781848900509, (Revised edition, 2013).
2. Kenneth Kunen (1980): Set theory: An Introduction to Independence Proofs. Elsevier Science, Amsterdam, Lausanne, New York, 1980, ISBN: 0-444-86839-9.
3. Justin Palumbo (0000): Forcing and Independence in Set Theory. Webpage, 0000, (UCLA Logic Center Summer School for Undergraduates).